Hugo A. Martin

Postdoctoral researcher
Équipe de recherche STEEP
Centre Inria de l’Université Grenoble Alpes
Laboratoire Jean Kuntzmann
Inria, 655 avenue de l’Europe,
38330 Montbonnot-Saint-Martin, France
martin_hugo[at]ymail.com
CV | Ecological Macroeconomics | Mechanics | Publications
(photo taken in 2022 on the Taillefer Massif)
Ecological Macroeconomics
Since my first postdoctoral position at Georgetown University (EJP), under the supervision of Gaël Giraud, I have been involved in mathematical modeling applied to ecological macroeconomics. My goal is to connect the economy to its biophysical environment to account for constraints from the physical world, as well as the short and long-term risks that our societies may face. I first have linked a macroeconomic model to a climate model. More recently, during my postdoctoral position at Inria (STEEP) under the supervision of Pierre-Yves Longaretti, I have been working on modeling financial speculation.
Modeling Financial Speculation in an Agent-Based/Stock-Flow Consistent (SFC) Model
I am working on a new Stock-Flow Consistent (SFC) model based on feedback loops that we have identified as crucial for representing systemic contagion risks, with a particular focus on the finance/speculation/energy aspect. Using these feedback loops, I have developed the CRISIS model, a hybrid Agent-Based (AB)/SFC model, where classical macroeconomic sectors (industry, households, banks, etc.) are disaggregated into networks of economic agents making decisions based on behavior rules specified by the modeler. This approach allows us to model a financial sector capable of taking speculative positions on energy assets, influencing their prices, and thereby affecting the solvency of industrial agents using them.
Gallery
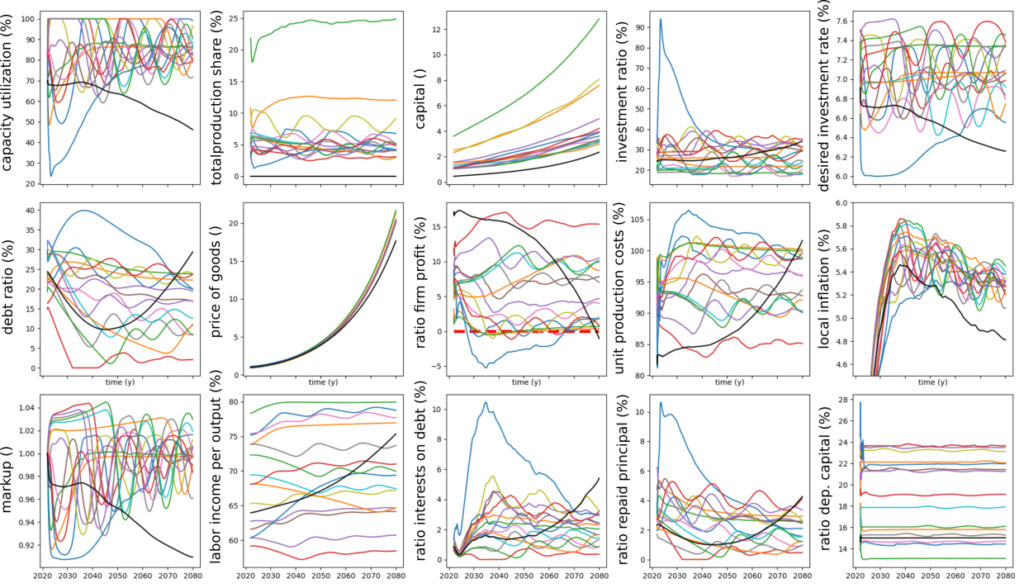
Business as Usual scenario
The model is currently mathematically formulated and implemented. This figure depicts a simulation parameterized to represent a « realistic » scenario where economic variables take reasonable values. The colored curves represent the trajectories of companies from the consumer goods production sector, while the black curve represents that of the energy product extraction sector.
Coupling of a Macroeconomic and a Climate Model
Designing effective climate change policies necessitates considering the intricate feedback loops between mitigation and adaptation. Increased mitigation efforts today can lead to lower adaptation costs in the future. Carbon taxes are often viewed as promising tools in this regard, but concerns exist about potentially burdening the private sector financially and depriving it of crucial economic resources. Conventional Integrated Assessment Models (IAMs) have limitations in analyzing the financial feasibility of mitigation-adaptation policies as they do not simultaneously incorporate economic growth, emissions, and damages. In response to this, we introduce the Integrated Dynamic Environment-Economic (IDEE) model, which couples an Earth Model of Intermediate Complexity with a non-linear macroeconomic model in continuous time. We then examine the simultaneous effects of carbon taxes and public spending on both climate and the global economy. Our analysis reveals that beyond a warming threshold of approximately +2.3°C, damages significantly increase the demand for additional investments in productive capital—an essential aspect of adaptation. This may potentially lead private firms into a scenario of debt overhang and trigger a worldwide cascade of defaults. Our findings suggest that the motivation behind the Paris Agreement target should not only be driven by climatic non-linearities and tipping points beyond the +2°C threshold but also by the emergence of tipping points. Additionally, we demonstrate that, with sufficiently high public subsidies, a tax of USD 300 per ton of CO2 equivalent by 2030 could enable achieving net-zero emissions by 2050. This approach helps prevent firms from experiencing global bankruptcy, emphasizing the importance of well-designed policy interventions.
Gallery
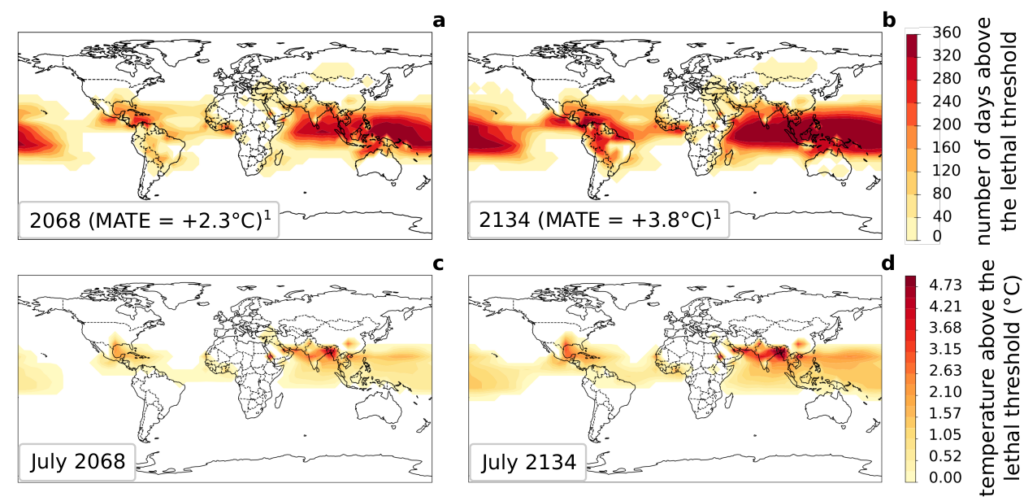
Deadly heatwaves
(a), (b) Maps represent the number of days spent above the lethal threshold as defined by Mora et al. (2017) in 2068 and 2134, which correspond to the years of the private-debt tipping points for the red and green trajectories. (c) (d) Maps represent the average relative surface air temperature above the lethal threshold for July of the same previous years.
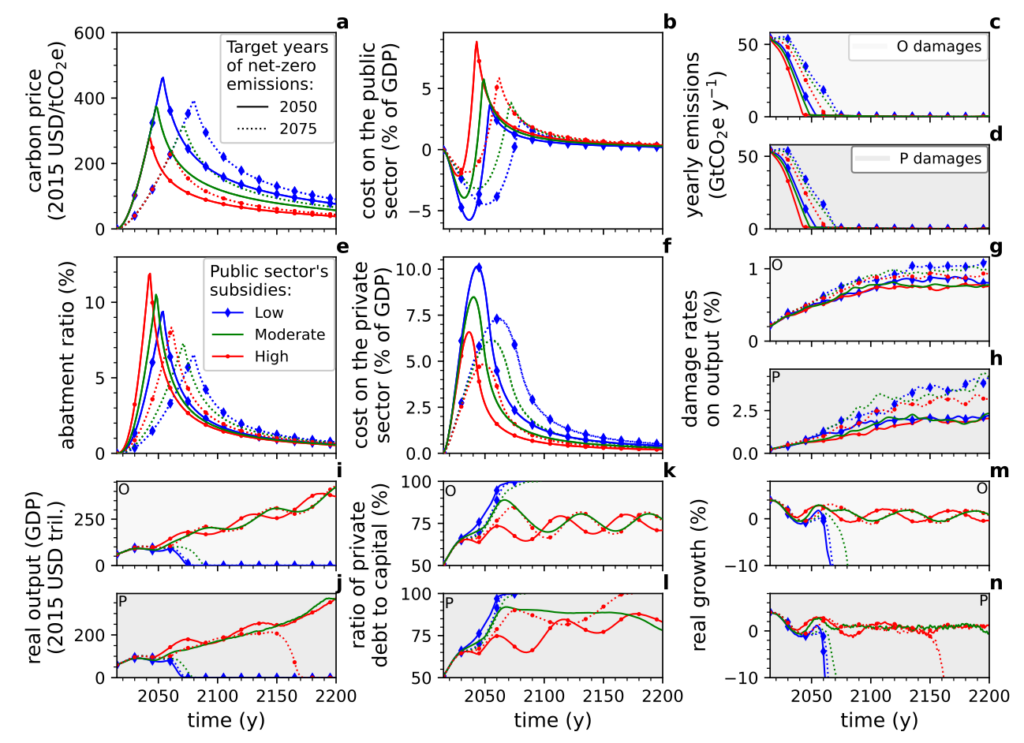
Evolution of the main IDEE’s variables with different levels of public policy
The solid (resp. dashed) curves correspond to two types of carbon prices aiming at net-zero emissions before the year 2050 (resp. 2075). The blue, green, and red curves correspond to the three levels of public sector involvement: 35%, 50%, and 65%, respectively, of abatement costs. The trajectories on lightgray (c), (g), (i), (k), (m) (resp. gray (d), (h), (j), (l), (n)) backgrounds have been computed with the optimistic (o) (resp. pessimistic (p)) damage function.
Mechanics – Modeling Granular Flows
The objective of my Ph.D. thesis made between Université Paris cité (IPGP) and Sorbonne Université (LJLL) (supervised by Anne Mangeney and Yvon Maday) was to study the destabilization processes of granular masses by ultrasonic waves (high frequencies (> 20 kHz) and low amplitudes (< 50 nm)), using mathematical modeling methods and numerical simulations. My first line of task involved mathematically incorporating the consideration of frictional effects within the framework of the convex optimization contact dynamics model COCD. We then validated the model and investigated erosion processes during flows on granular beds by comparing our results with experiments. Secondly, we compared our simulations with those of the continuous models: Basilisk (Navier-Stokes) and SHALTOP (thin-layer). I finally propose a multiscale numerical modeling approach that examines dense granular flows triggered by acoustic waves in granular layers excited by the inclined basal plane.
Convex Optimization Contact Dynamics (COCD) and Simulations on Erodible Beds
Erosion processes and the corresponding static/flowing transition in granular flows remain poorly understood, despite their critical role in natural hazards like landslides and debris flows. Continuum models currently struggle to adequately capture observed phenomena such as the increased runout distance of granular flows on erodible beds or the development of waves at the bed/flow interface. Discrete Element Methods (DEM), which simulate individual grain motion and complex interactions, offer a unique numerical tool to investigate these processes. Convex Methods (CM), derived from convexification of Contact Dynamics methods, present a robust theoretical framework ensuring numerical solution convergence at each time iteration. They also exhibit intrinsic stability superior to classical Molecular Dynamics methods. While implemented in engineering fields, CMs have not yet been tested for flows on erodible beds. This study introduces a Convex Optimization Contact Dynamics (COCD) method, demonstrating its ability to generate a numerical solution adhering to Coulomb’s law at each contact and iteration. Following calibration and validation against experiments and another widely used Contact Dynamics method, our simulations accurately replicate qualitative and numerous quantitative features of experimental granular flows on erodible beds. These include the runout distance increase with erodible bed thickness, spatiotemporal changes in the static/flowing interface, and the presence of erosion waves behind the flow front. Beyond erosion processes, our findings endorse CMs as potentially accurate tools for exploring complex granular mechanisms.
Gallery
2D Study of Flow Initiation at Door Opening
The simulation depicts a dam break, but in this video, only the lower part below the door opening is represented. The color represents the translation speed of the grains. The grains have a diameter of 0.7 mm, and the simulation involves a granular mass of 60,000 particles.

Simulation of 120 000 grains on a rough plane.
The granular assembly is composed of spheres (with 10% of polydispersity) and the flow is confined by two invisible lateral walls and another wall located at the left of the domain. Concerning the bottom, the rough bed is composed of glued spheres with the same grain properties and polydispersity. In this film the colors represent the normalized velocity of translation.
Real time column collapse
This simulation has been used to compare COCD (inelastic) with the well know method NSCD (elastic). The mass profiles simulated with the two methods are very close. It shows that considering a purely inelastic model provides sufficient approximation of the flow dynamics, especially in the context of column collapses.

Kelvin-Helmholtz like instabilities
We investigate here as to whether the Kelvin-Helmholtz conditions are fulfilled in this simulations. The flowing and erodible layers can be assimilated to two different fluids of different densities, and different down-slope velocities. In fluids, a slight perturbation at the interface is amplified by the local velocity difference and a corresponding local decrease of the flow pressure. If the velocity of the superjacent fluid is sufficient, the amplified perturbation transforms into a breaking wave.
Comparison Between Discrete Element, Navier-Stokes, and Thin-Layer Models
Granular flows manifest in diverse contexts, encompassing laboratory experiments, industrial processes, and natural geophysical phenomena. Various physically based models have been developed to explore their dynamics, distinguished by the length scale at which dynamic processes are described. Discrete models operate at a microscopic scale, modeling individual grains; Navier-Stokes models use a mesoscopic scale, considering elementary volumes of grains; and thin-layer models employ a macroscopic scale to capture the dynamics of elementary columns of fluids. While the derivation of associated equations is well-established for each, limited attention has been given to the coherence of results among these modeling approaches. In this study, we compared simulations of a granular dam break on horizontal or inclined planes using the discrete model Convex Optimization Contact Dynamics (COCD), the Navier-Stokes model Basilisk, and the thin-layer depth-averaged model SHALTOP. Our findings reveal that, although all three models reproduce the temporal evolution of the free surface in the horizontal case (except for SHALTOP at initiation), the modeled flow dynamics differ significantly, especially during the stopping phase. While stresses at the flow’s bottom, reflecting flow dynamics, show relatively good agreement, the COCD model introduces notable variations due to complex and rapidly changing granular lattices. Similar conclusions arise when using the same rheological parameters to model a granular dam break on an inclined plane. This comparative analysis is crucial for evaluating the limitations and uncertainties inherent in granular flow modeling.
Gallery
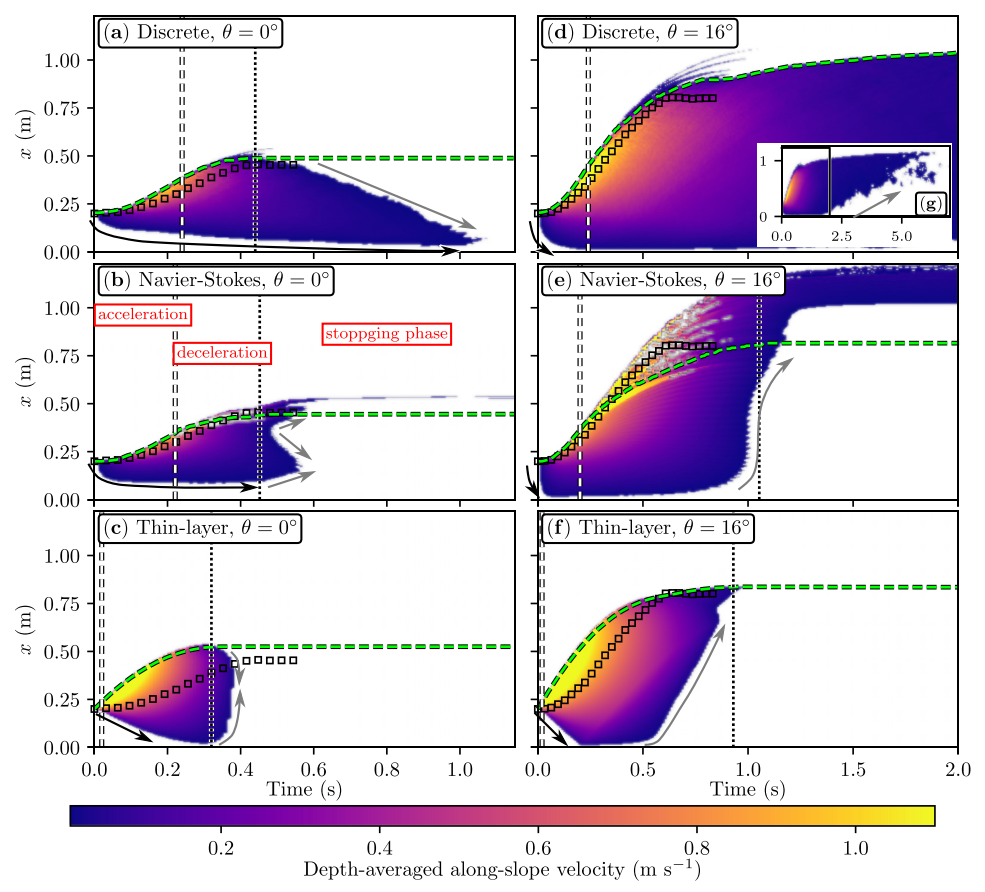
Spatiotemporal plot representing the depth-averaged along-slope flow velocity Vx (color scale) for the different models.
For each simulation, the green dashed line represents the time evolution of the front position. The acceleration and deceleration θ = 0° (a)–(c) and θ = 16° (d)–(f). We only display velocities above 1 cm s−1 (lower velocities are represented in white), as in the experiments phases are separated by a vertical white dashed line, and the deceleration and stopping phases by a vertical black dotted line. Black arrows follow the rarefaction wave where the mass initially at rest is set in motion. Grey arrows follow the stopping wave where the moving mass stops. Black squares give the front position in experiments.
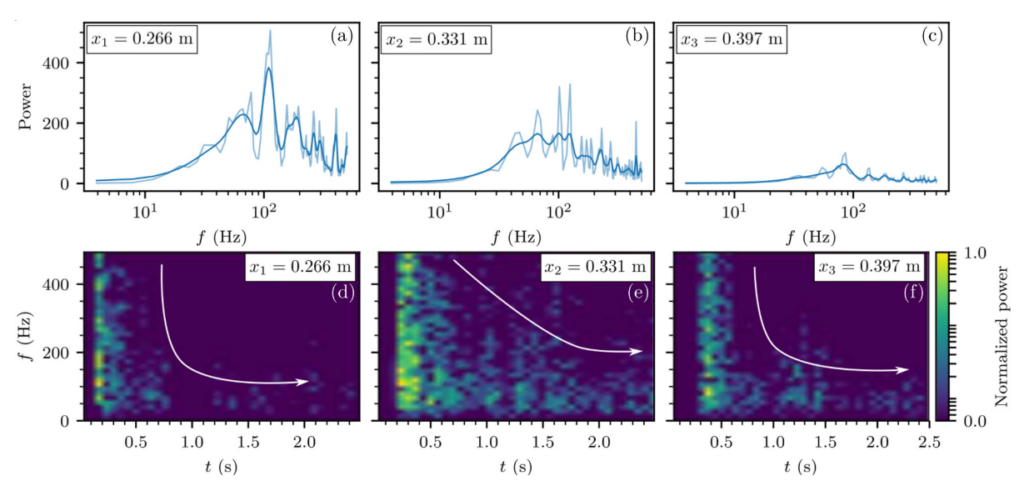
Spectral content of the discrete (COCD) basal normal stress
At θ = 0◦ computed at x1 = 0.27m (a), (d); x2 = 0.33m (b), (e); and x3 = 0.40m (c), (f). The first line (a)–(c) is the spectral amplitude (light blue line: raw Fourier transform; dark blue line: smoothed Fourier transform). The second line (d)–(f) displays the corresponding spectrograms.
Modeling Ultrasound in Dense Granular Flows
Understanding the mechanisms behind the remote and local triggering of landslides and earthquakes by seismic waves at micro-strain amplitude is essential for quantifying seismic hazards. Granular materials, existing in an out-of-equilibrium and metastable state, offer a relevant model system to explore landslides and fault dynamics within the unjamming transition framework, transitioning from solid to liquid states. Recent laboratory experiments have indicated that ultrasound-induced interfacial sliding or granular avalanches may be linked to a reduction in interparticle friction through shear acoustic lubrication of contacts. However, investigating crack growth or slip at the scale of grain contacts within an optically opaque granular medium remains a challenging issue. To address this challenge, we propose a multiscale numerical modeling approach that examines dense granular flows triggered by acoustic waves in 2D granular layers excited by the inclined basal plane. We perform numerical simulations of ultrasonic vibrations in the millisecond range and the onset of flows in the second range, respectively. Our primary focus is on correlating local rearrangements at the grain scale with the onset of continuous flows at the macroscopic scale. This onset results from the decrease in the interparticle friction coefficient induced by shear acoustic lubrication. A key finding is that ultrasound primarily propagates through the strong-force chains, while the decrease in interparticle friction induced by ultrasound occurs in the weak contact forces perpendicular to the strong-force chains. This decrease in interparticle friction initiates local rearrangements, eventually leading to a continuous flow through a percolation process with a delay depending on the proximity to failure. In comparison to gravity-driven flow, ultrasound-induced flow appears much more uniform in space, indicating the role of an effective temperature due to ultrasonic vibration. We also validate these simulations by comparing them with experimental observations of granular flows triggered by ultrasound below avalanche angles, demonstrating the validity of our numerical method.
Gallery

Propagation of a perturbation on a contact network
An initial perturbation of the position of a single grain within the granular assembly propagates over time throughout the domain, passing through the contacts between grains. This solution is obtained by solving the unsteady wave equation. For visualization purposes, the displacement of the grains is amplified by 10,000 times.
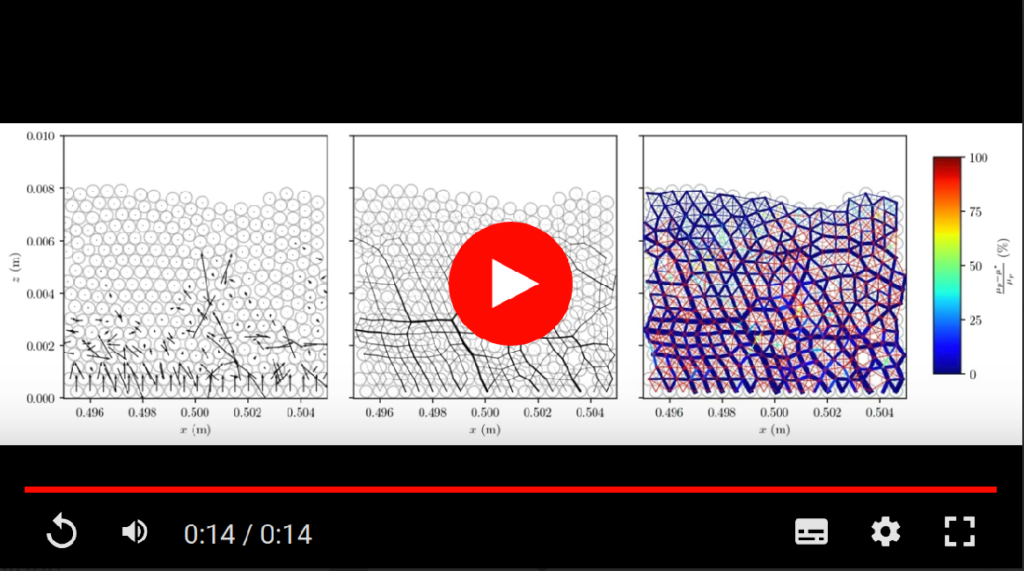
Unltrasound-induced friction pertubation
(left) Vibration-induced displacements, (midle) contact force chains, and (right) rate of vibration-induced perturbation of the interparticle friction, for θ=15°, H/d = 14.4, f = 70 kHz. On the left, the black arrows represent the computed vibration-induced displacement. On the midle, the black lines represent the force chains formed between the grains on a linear scale. On the right, the lines between grains represent the force chains on a logarithmic scale, and the color map represent the rate of decrease in interparticle friction coefficients.

Effect of Ultrasonic Basal Vibrations on Flow Initiation
The flow at the top is simulated without ultrasonic vibrations. The flows in the middle and at the bottom are simulated with basal ultrasonic vibrations, and larger oscillation amplitudes are used for the bottom flow (U0 = 60 nm compared to 100 nm). All these simulations are conducted on a slope of 16°. The colors represent the translational velocity of the grains. The film highlights the ability of the waves to trigger flow more easily and to homogenize the initiation throughout the domain.
Publications
- Martin, H. A., Delannoy, L., Longaretti, P. Y. & Prados, E. (2024). Macroeconomics and finance coupled modeling for short– and mid–term crises. Working paper. Article (available in MyBox at codes_INRIA/crisis_working_paper.pdf)
- Martin, H. A. & Longaretti, P. Y. (2024). A variance-based sensitivity analysis of a Goodwin-Keen type economic model. Working paper.
- Martin, H. A., Mangeney, A., Jia, X., Maury, B., Lefebvre-Lepot, A., Maday, Y., & Dérand, P., Ultrasound-induced dense granular flows: A two-time scale modeling. (2024). In review in Journal of Fluid Mechanics. Article.
- Martin, H. A., Quiquet, A., Nicolas, T., Giraud, G., Charbit, S., & Roche, D. M. (2023). Climate-Induced Economic Damages Can Lead to Private-Debt Tipping Points. In review in Communications Earth & Environment. Article.
- Martin, H. A., Mangeney, A., Lefebvre-Lepot, A., Maury, B., & Maday, Y. (2023). An optimization-based discrete element model for dry granular flows: Application to granular collapse on erodible beds. Journal of Computational Physics, 498, 112665. Article.
- Martin, H. A., Peruzzetto, M., Viroulet, S., Mangeney, A., Lagrée, P. Y., Popinet, S., Maury, B., Lefebvre-Lepot, A., Maday, Y., & Bouchut, F. (2023). Numerical simulations of granular dam break: Comparison between discrete element, Navier-Stokes, and thin-layer models. Physical Review E, 108(5), 054902. Article.
- Bailly, H., Guitonneau, C., Jacques, P., Martin, H. A., Valcke, P., & Verzier, F. (2022). Modéliser l’économie dans l’environnement Des concepts aux données: une modélisation sous contraintes. In Conférence Archipel 2022: Risques systémiques, trajectoires et leviers d’action transdisciplinaires. Inproceedings.
- Martin, H.A. (2019). Convex contact dynamics methods with friction: granular flow and generated elastic waves. Université Paris Cité. Ph.D. thesis.


